More on Bezier Path
在之前讲解 Icon Font Viewer 和 SVG 的文章中,曾经简单介绍过 Bezier Path。 这次再稍微介绍一点数学原理,另外针对 Bezier Path 使用上的一些问题进行更多的探讨。
贝塞尔曲线最初应用于汽车主体设计,由法国工程师 Pierre Bézier 最早提出。 现在在计算机图形学中具有的应用非常广泛,可以说, 你在计算机上所看到的大多数矢量曲线,都是由 Bezier Path 绘制出来的。
目前常用的 Bezier 曲线有二阶和三阶两种。广泛使用的 TrueType 以二阶 Bezier 曲线为基础的, Postscript 则是使用三阶 Bezier 曲线的代表。三阶 Bezier 曲线已经可以满足大多数需求了, 对于更高阶的曲线,可以使用这两种 Bezier 曲线来进行分段拟合。
下面先介绍 Bezier 曲线的数学表达式。
Bezier 曲线的数学表达式
最简单的 Bezier 曲线是一阶的——其实就是线段。它的参数形式是:
$$\mathbf{B}^{(1)}(t)=\mathbf{P}_0 + (\mathbf{P}_1-\mathbf{P}_0)t=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1]$$
观察上面的公式,在$t$取0到1之间的值时,$\mathbf{B}(t)$的值就是在$\mathbf{P}_0$和$\mathbf{P}_1$之间线段上某一点的坐标。 我们把$\mathbf{P}_0$和$\mathbf{P}_1$称为曲线的控制点,那么一阶 Bezier 曲线需要的控制点数量就是2。 实际上,$n$阶 Bezier 曲线需要$n+1$个控制点。
一阶 Bezier 曲线还称不上“曲线”,使用最多的两种 Bezier 曲线是二阶和三阶的。 二阶 Bezier 曲线的参数方程为:
$$\mathbf{B}^{(2)}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } t \in [0,1]$$
三阶 Bezier 曲线的参数方程为:
$$\mathbf{B}^{(3)}(t)=\mathbf{P}_0(1-t)^3+3\mathbf{P}_1t(1-t)^2+3\mathbf{P}_2t^2(1-t)+\mathbf{P}_3t^3 \mbox{ , } t \in [0,1]$$
对于$n$阶的 Bezier 曲线,有一个一般化的参数方程,这里就不再赘述。 在目前的使用的计算机图形绘制系统中,最广泛使用的就是三阶 Beizer 的曲线, 因为它的复杂度比较适中,尤其是用来拟合圆弧的时候非常方便, OSX 和 iOS 的绘图系统 CoreGraphic 就是使用的三阶 Bezier 曲线, SVG 标准上来说同时支持二阶和三阶 Bezier 曲线,但是不同浏览器在绘制的时候可能会有所不同。
下面有两个重要的性质在后面的讨论中可能会用到:
- $n$阶 Bezier 曲线经过它第一个控制点和最后一个控制点。 只需要$t$分别设为$0$和$1$就可以看出来。
- 对于二阶以上的 Bezier 曲线, $\mathbf{P}_0\mathbf{P}_1$ 和 $\mathbf{P}_{n-2}\mathbf{P}_{n-1}$ 这两条线段同曲线相切。
- $\mathbf{B}(t) = (1-t)\mathbf{B}(t) + t\mathbf{B}(t)$
使用高阶 Bezier 曲线拟合低阶 Bezier 曲线。
之前曾经提到过,一些图形系统只支持某一个阶次的 Bezier 曲线, 比如 PostScript 和 Cocoa 就只支持三阶 Bezier 曲线。但是有些图形系统, 比如 TrueType 和 SVG,都是支持 二阶 Bezier 曲线的。 因此我们需要能够在只支持高阶 Bezier 曲线的图形系统中绘制低阶 Bezier 曲线。
实际上利用上面的第三个属性,这件事是可以精确做到的(每个点都可以相吻合)。 这里只给出二阶升三阶的过程:
对于二阶 Bezier 曲线 $\mathbf{B}^{(2)}(t)$,将其表达式带入第三条性质,有
$$\begin{eqnarray*} \mathbf{B}^{(2)}(t) & = & (1-t)\mathbf{B}^{(2)}(t)+t\mathbf{B}^{(2)}(t)\\ & = & (1-t)^{3}\mathbf{P}_{0}+(1-t)^{2}t\mathbf{P}_{0}+2(1-t)^{2}t\mathbf{P}_{1}+\\ & & 2(1-t)t^{2}\mathbf{P}_{1}+(1-t)t^{2}\mathbf{P}_{2}+t^{3}\mathbf{P}_{2}\\ & = & (1-t)^{3}\mathbf{P}_{0}+3(1-t)^{2}t\frac{\mathbf{P}_{0}+2\mathbf{P}_{1}}{3}+\\ & & 3(1-t)t^{2}\frac{2\mathbf{P}_{1}+\mathbf{P}_{2}}{3}+t^{3}\mathbf{P}_{2} \end{eqnarray*}$$
取下列变换代入原式
$$\begin{eqnarray*} \mathbf{P}’_{0} & = & \mathbf{P}_{0}\\ \mathbf{P}’_{1} & = & \frac{\mathbf{P}_{0}+2\mathbf{P}_{1}}{3}\\ \mathbf{P}’_{2} & = & \frac{2\mathbf{P}_{1}+\mathbf{P_{2}}}{3}\\ \mathbf{P}’_{3} & = & \mathbf{P}_{2} \end{eqnarray*}$$
恰好可以得到三阶 Bezier 曲线$\mathbf{B}^{(3)}(t)$的表达形式。这样我们就可以使用三阶 Bezier 曲线来精确绘制出二阶 Bezier 曲线。也正因为如此,在目前绝大部分的计算机图形系统中,都是只提供三阶 Bezier 曲线的绘制函数。
下面是一个使用 SVG 绘制的例子(需浏览器支持才能查看),你可以通过查看页面源码看到具体的实现。 从左往右,依次是二阶 Bezier 曲线、三阶 Bezier 曲线和将二者重叠起来的效果。可以看到两条曲线是完全吻合的。
用低阶曲线表示高阶曲线?
接下来自然有一个问题,如果我有一个高阶的曲线需要绘制,而系统只支持低阶曲线,那么应该如何实现呢? 很不幸的是,使用有限条低阶的曲线是没有办法精确的绘制出需要的高阶曲线的,一般使用的方法是逼近法。 一个比较常用的技巧是将高阶曲线分割为两个部分,对这两个部分分别使用低一阶的曲线进行逼近,从而获得一个比较好的效果。
关于这个主题,这篇文章 中有详细的介绍,涵盖了:
- 使用一条低阶曲线逼近高一阶曲线的方法
- 使用两条曲线逼近高一阶曲线前后两部分的方法
- 可变数量的曲线动态逼近高一阶曲线的算法
使用低阶曲线逼近高阶曲线是一个比较复杂的问题,而且没有一个很简洁且效果很好的通用公式。 这里就不赘述了。
一个更实用的方法是直接用折线去逼近高阶曲线。实际上,即使是二阶和三阶 Bezier 曲线, 具体实现中也是使用同样的方法。既然知道了高阶曲线的参数方程,直接使用方程来分段成折线绘制自然最好不过了。 需要注意的是,为了获得较好的效果和性能,一般来说不会使用均匀的折线分段。 一个比较简单的算法就是在曲线曲率较大的地方多安排分段,反之少安排分段。
使用三阶 Bezier 曲线逼近圆弧
圆弧是另一个我们经常使用的平面曲线,下面是圆的参数方程:
$$ \begin{eqnarray*} x=r\cos\theta\\ y=r\sin\theta \end{eqnarray*}. $$
可以看出,如果要精确绘制圆弧,我们不得不计算$\sin\theta$和$\cos\theta$的值, 这对于计算机来说,是一个成本很高、得不偿失的工作。使用具有多项式表达式的三阶 Bezier 曲线来逼近圆弧就成为了一个很好的选择。
我们是无法使用一条完整的 Bezier 曲线来绘制整个圆的,常用的方法是用一条 Bezier 曲线去逼近一个四分之一圆弧, 使用四条曲线组成一个圆。
简便起见,取圆心在原点的单位圆在第一象限的四分之一圆弧进行讨论。由上面所提到的 Bezier 曲线的第一条性质,可以得到用来用来逼近这个圆弧的 Bezier 曲线一定满足:
$$ \begin{eqnarray*} \mathbf{P}_{0} & = & (0,1)\\ \mathbf{P}_{3} & = & (1,0) \end{eqnarray*} $$
这是因为我们指定的圆弧必定经过$(0,1)$和$(1,0)$这两个点,因此用来逼近的 Bezier 曲线也应该经过这个点。
同理,因为圆弧在这两点的切线分别平行于$x$轴和$y$轴,由第二条性质,$\mathbf{P}_1$的$x$坐标必定为$1$, $\mathbf{P}_2$的$y$坐标必定为$1$。同时因为圆弧是对称的,$\mathbf{P}_1$的$y$坐标和 $\mathbf{P}_2$的$x$坐标一定是相同的,将其设为$\lambda$,此时 Bezier 曲线的表达式可以化简为:
$$ \begin{eqnarray*} C_{x}(t) & = & 3(1-t^{2})t\lambda+3(1-t)t^{2}+t^{3}\\ C_{y}(t) & = & (1-t)+3(1-t^{2})t+3(1-t)t^{2}\lambda \end{eqnarray*} $$
其中$C_{x}(t)$和$C_{y}(t)$分别代表三阶 Bezier 曲线的$x$和$y$坐标关于参数$t$的函数。
此外,我们的圆弧肯定经过$(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$这个点, 使 Bezier 曲线经过这个点,且由对称性此时需有$t=0.5$。 代入上面的式子,我们可以解出。
$$ \lambda = \frac{4}{3}(\sqrt{2}-1)\approx 0.5522847498 $$
至此我们就可以绘制出来一个比较完美的四分之一圆弧了,为了绘制一整个圆, 可以使用四个这样的 Bezier 曲线来实现。不同半径的圆只要按比例缩放上面这个参数就可以达到目的。 实际上使用三阶 Bezier 曲线,我们还可以方便的绘制出非$\frac{\pi}{2}$弧度的圆弧。 具体的公式可以在这个参考文献中找到。
下面是一个使用 SVG 的绘制演示,最左边是使用三阶圆弧绘制的效果,中间是使用 SVG 内置的 Arc 命令绘制的效果, 最右边的是将两个结果重叠在一起的效果,可以看出来是完全吻合的。这是因为在绝大部分 SVG 的绘制系统中, 其实就是使用三阶 Bezier 曲线来绘制圆弧的。
总结和扩展
在这篇文章讨论了二维平面上的 Bezier 曲线的一些特性,只要改变控制点的维度, 就可以很容易地将其推广到三维甚至更高维空间上去。
现在,在 Bezier 曲线的基础上还发展出了 B 样条,并能够进一步推广为 NURBS (非均匀有理B样条)。 NURBS 在 3D 建模和工业设计上使用非常广泛,常用的 3D 制作软件,如 Maya、Rhino、Blender 等都支持 NURBS。 下图是在 Blender 中显示一个简单 NURBS 表面的效果。
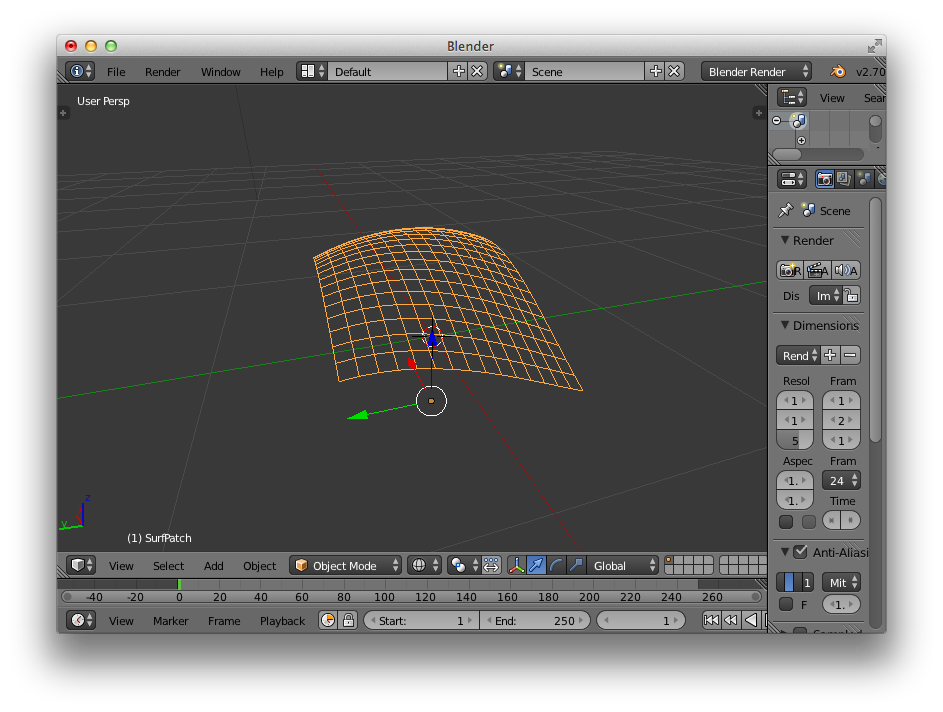
关于 Bezier 曲线还有很多值得讨论的东西,希望这篇文章对相关学习提供一定的帮助。
