从 Immutable 到 Log-Structured Merge Tree
说起 Immutable Data Structure,浮现在人们脑海里的可能是 Scala 和 Clojure 或者 ImmutableJS 等语言和库所提供的数据结构。不过,今天这篇文章则是想要通过介绍实现不可变数据结构的一些思路, 带领大家了解另一种具有巨大应用价值的数据结构:Log-Structured Merge Tree。
Immutable Data Structure
在很多编程语言当中,都包含一些不可以被修改的数据结构,比如 Python 里的字符串和元组类型等。 这些数据类型都不能进行修改操作。或者说,每次修改这类对象,都会得到一个新的对象, 而原来的对象不会被改变。这样的数据结构我们称为不可变数据结构(Immutable Data Structure)。
不可变数据结构在很多方面都拥有重要的应用价值,比如说:
- 实现撤销功能。由于不可变数据结构每次操作都产生新的对象,那么一个简单的想法就是我们可以将多个修改产生的对象组织起来, 在实现撤销时直接通过调出之前的对象来恢复原来的状态
- 在函数式编程的范畴里,因为对不可变数据结构的操作都会产生新的对象,因此以它们为参数调用函数不会产生副作用, 这样的特性既满足了函数式编程的要求,也降低了程序因副作用产生难以调试的 Bug 的可能性
- 在并发编程中,得益于不可变数据结构的稳定性,避免了共享访问时的互斥问题,在很大程度上可以降低并行程序设计的难度。 稍后我们还会看到,不可变数据结构还是无锁数据结构实现的一种重要思路
- 不可变数据结构因其不可变的特性,在进行树形比较的时候可以简化比较操作的次数,提高比较的性能。 适用于 React 应用的 ImmutableJS 就利用了这一点
Python 中的字符串和元组类型在每次修改时都会复制自身从而产生新的对象。 这种实现方法虽然比较简单,但是在时间和内存空间的消耗上都比较大。像 Scala 和 Clojure 这样的编程语言实现了更为复杂的数据结构(如 Vector Trie 或 HAMT),从而使得修改之后的对象可以节约很多内存空间, 在性能上也不会有太大的损失。
在这里我们不讨论 Immutable 数据结构具体的实现细节,而是通过两个简单的例子来介绍这类数据结构实现的简单思路。 稍后我们还会看到,版本控制工具 Git 的内部实现中就恰好应用了这两个技巧。
Immutable Stack
首先来看第一个例子。我们知道 Stack (栈)是一种先进后出的容器,它支持两种基本操作:
- 在栈顶插入一个元素
- 从栈顶取出一个元素
在这个基础上,我们想要实现另外两个功能,从而使得我们的栈具有实现撤销功能(或者说快速查询之前版本的能力)。 具体来说就是:
- 每一次插入和删除操作之后,可以为当前栈中元素的内容指定一个 History ID
- 指定之前的某一个 History ID,可以快速的恢复栈在那一时刻包含元素的状态
这一问题看似不好下手,其实在采用链表来实现栈的情况下,有很优雅的解决方案。 下图展示了一个由链表表示的空栈:

接下来我们向栈中压入几个元素,得到的栈的状态如下:
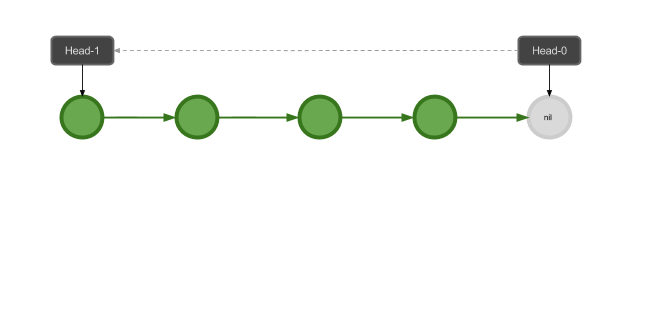
那么出栈操作怎么实现呢?我们把指向栈顶的头向后移动几个元素就可以了:
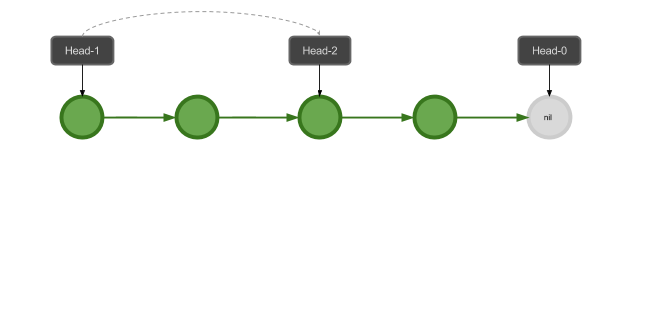
从新的位置开始插入其它的元素呢?其实只是在栈中开启一个新的分支:
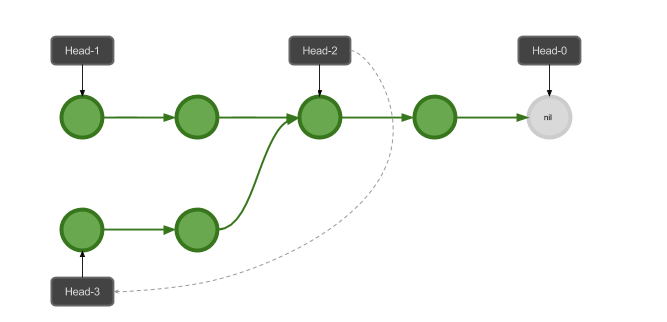
可以看到,我们的 Immutable Stack 相比传统链栈的实现,唯一的区别就是每次改变 HEAD 指针的时候, 我们都用构造一个新的指针来代替,这样通过原来的 HEAD 指针,我们访问到的总是栈在原来时刻的状态, 而从新的指针开始,得到的就是新的状态了。
这一实现方案可以说是相当优雅的。为了实现纪录历史的功能,我们每次操作只多消耗一个 HEAD 指针的空间。 我们把这些 HEAD 指针保存在某一容器中,未来就可以通过其与 History ID 的对应关系来查找它们, 而恢复一个 History ID 所指代的状态快照,只需要从对应的 HEAD 指针开始访问就好了,是一个非常省时且简单的操作。
Immutable Tree
接下来研究第二个例子。树结构可以说是计算机程序当中非常常用的一种数据结构,文件系统、数据层级等等的表示都依赖于树的实现。 下图展示了一棵用于表示文件系统的树。
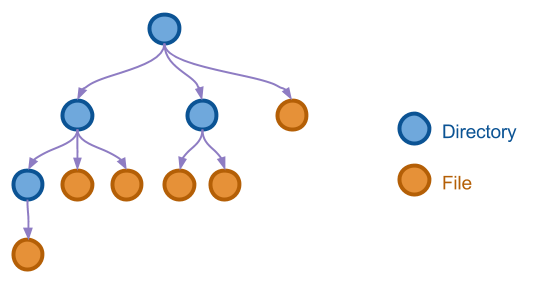
为简便起见,我们假定树的基本操作是如下的三种:
- 在树的某个位置添加一个新的节点
- 删除树的某个叶子节点
- 修改树的某个节点
在很多应用中,除了上面的三种操作,撤销功能也是非常重要的。也就是说,我们有时候想要容易地将树的状态恢复到之前的一个纪录。 如前文所述,由于不可变数据结构每次都会产生新的对象,它的一大应用就是实现撤销的功能。但是对于一棵树来说, 如果每次都把每个节点复制并保存下来,在时间和空间花费上都非常不经济。这个问题就是我们的 Immutable Tree 数据结构要解决的问题。
下图展示了解决空间消耗问题的一种思路:
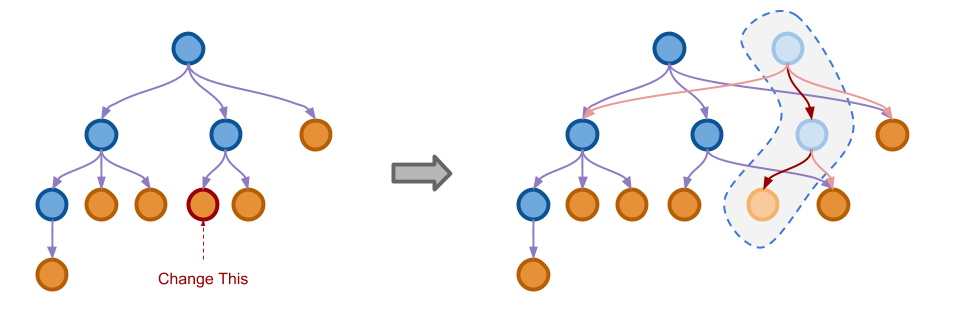
可以看到,当左边树的一个叶子节点被修改之后,我们既不全盘复制所有的节点,也不在原来的节点上进行修改, 而是仅仅将被修改位置一直到根节点的一条路径复制出来再进行修改。在右边虚线圈中的几个节点就是新生成的节点, 这些节点仍然会有指向原来节点的指针,只有被修改路径上的指针是指向新的节点。
使用这种技巧,每次我们只会复制一条路径上的几个节点,比复制全部节点已经有很大提高了。 新产生的对象和原来的对象共享了绝大部分内部节点,而每次修改一定会产生一个新的根节点。 使用不同的根节点作为开始,我们访问到的就是树在不同时刻的状态。
这种利用树形结构的特点来共享内部节点是绝大部分不可变数据结构的基本原理,譬如 Scala、Clojure 和 ImmutableJS 实现的 Vector Trie 和 HAMT 本质上就是树形结构。
案例研究: Git 的对象模型
在看完上面的文章之后,对 Git 比较熟悉的朋友可能已经发现了这两个数据结构和 Git 的相似之处。 诚然,Git 这样的版本控制系统恰巧需要实现的就是文件系统历史状态的纪录和恢复。
打开任意一个 Git 仓库,我们会发现仓库下有一个名为 .git 目录,这个目录的简单结构如下:
1 | .git |
其中的objects目录就是 Git 储存自己的内部数据对象的位置。无论是被 Commit 过的文件、一个 Commit
对象还是对目录结构的描述都存放在这个地方。在执行 Git 的版本切换和查询操作的时候,Git
就是从这个目录当中读取数据重建历史状态的。
如果直接读取这个目录下面文件的内容,会发现它们都是二进制,这是因为 Git 对这些内容进行了压缩。 我们可以使用下面的命令快速地获取某个 Hash 值所代表的对象的内容:
1 | git cat-file -p 5b67fd90081 |
接下来我们来看一个非常简单的 Git 仓库,它的提交历史如下图所示:
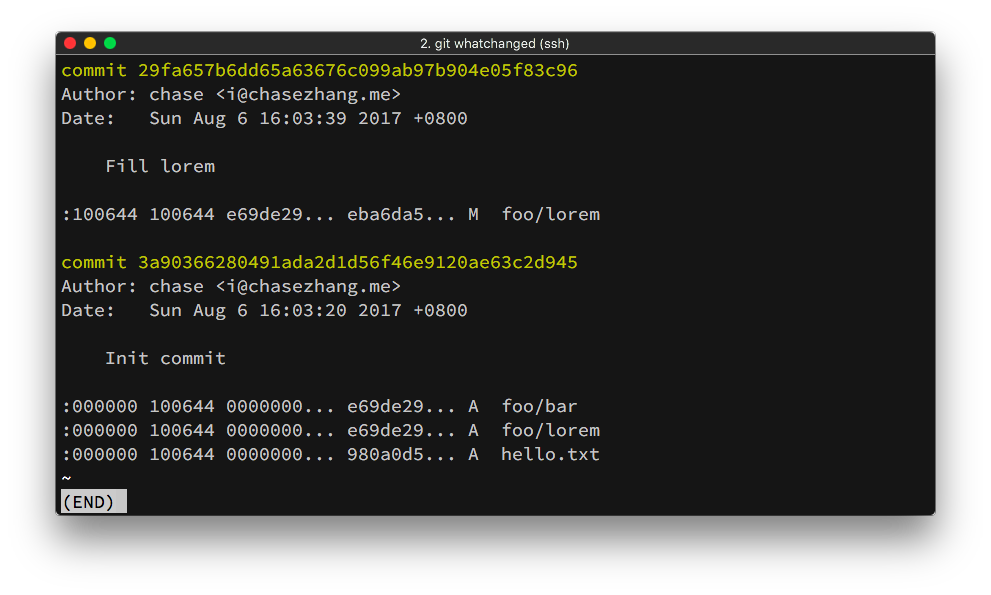
在第一个 Commit 里我们添加了一个文件hello.txt和一个文件夹foo,
文件夹foo下面还有两个文件bar和lorem。在第二个 Commit 当中,我们修改了文件foo/lorem。
接下来如果我们使用git cat-file -p 29fa657b6dd65a6命令来查看最新的 Commit,将会得到如下的内容:
1 | tree b0b36b9811c2bd5a208a263236518628972ed32a |
从上面的内容可以看出,一个 Commit 除了纪录作者和 Commit Message 之外还有两个重要的字段,
tree和parent。其中parent字段给出的 Hash 值恰好和这个 Commit 前一个Commit 的值相同,
它就是每个 Commit 指向上一个 Commit 的指针。那么tree字段的作用是什么呢?
我们使用git cat-file -p b0b36b9811c2来查看一下他的内容:
1 | 040000 tree 91288d89327ac71ad84fa4eb08586b2b78d8cafb foo |
可以看出这个对象给出了当前文件目录的一个描述,其中子目录foo仍然是一棵树,而hello.txt是一个文件。
前面提到,第一个 Commit 和第二个 Commit 只有foo/lorem这个文件修改了,那么 Git 是如何纪录这个修改的呢?
我们来看第一个 Commit 的 tree 字段的内容:
1 | 040000 tree 2c90d818605361f15a66019953e13fdf86aacf6c foo |
两相对比,没有改动的hello.txt在两个 Commit 对应的 Tree 里指向的都是同一个对象,
而foo文件夹则指向了新的对象(Hash 值不同)。如果近一步查看foo目录,也会观察到类似的现象。
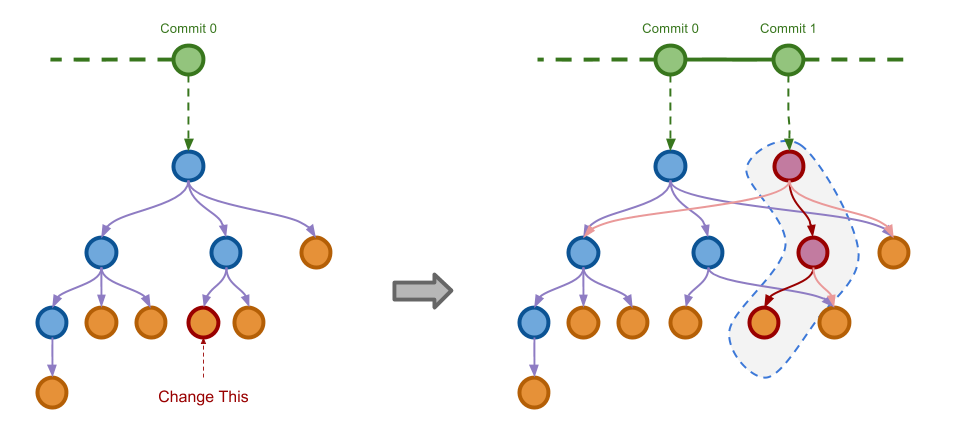
也就是说,Git 的内部对象的组织,就是利用了前面介绍的两个简单的算法。Git 的 Commits 就对应于 Immutable Stack,
而 Git 的文件系统就是使用 Immutable Tree 来纪录的。
Lock-free Data Structure
为了讨论我们最终的主题,关于无锁数据结构(Lock-free Data Structure)的一些知识是必要的。
简单来说,无锁数据结构是一类可以安全地使用多线程并发访问和修改的数据结构, 而它们从设计上避免使用锁这一同步工具,在某些应用场合下相比使用加锁的数据结构具有更好的访问性能, 也避免了因为锁的存在而产生的死锁和 CPU 停顿问题,因此被广泛应用于强并发、高实时性要求的领域。
无锁数据结构是一个非常大的主题,有多种多样的实现方法,在这里无法详尽的叙述。 在本文的语境下,主要关注的是一类通过结合不可变数据结构和编程语言当中原子操作这种同步工具的实现方法。
原子操作是由编程语言或者操作系统提供的一系列同步元语。一个原子操作在执行的时候被认为是原子的,
也就是说它要么能够成功之行,要么执行失败。一个典型的例子是CompareAndSet元语,
这个原子操作将一个变量的当前值和某一指定值进行比较,如果结果相同,则将这个变量设为另一个值。
很显然,如果是简单地使用判断语句进行判断,在并发执行的时候并不能保证结果的有效性。
这是因为比较操作和赋值操作是两个独立的操作,另外一个线程可能恰好在比较成功之后、变量赋值之前修改了目标变量的值。
因此,提供一个原子操作来实现这一功能是很有价值的。
那么,原子操作是怎么和不可变数据结构结合起来的呢?以前文的 Immutable Tree 为例, 首先我们使用一个原子引用类型的指针指向一个 Immutable Tree 的对象,使得所有对这一对象的访问都要通过这一引用, 如下图所示:
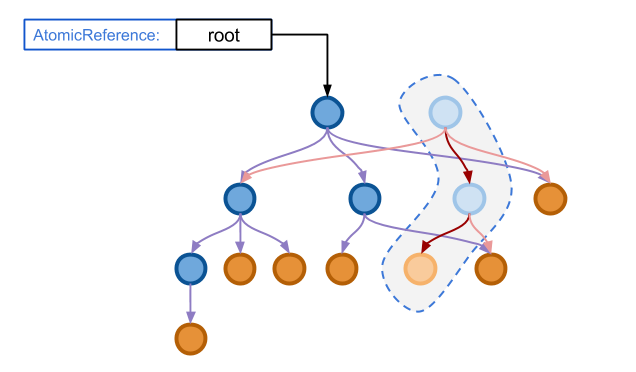
由于对于 Immutable Tree 的任何修改操作都不会改变原来的节点。 因此,如果有一个对树的修改操作到来,我们可以安全地开始对树的操作而不需要对整个数据结构加锁, 这一修改完全是平行于原来的数据结构,因此对于读操作没有任何阻塞。
当修改完成之后,我们可以对我们的引用执行一个原子的交换操作,从而使他指向新的根节点,如下图所示:
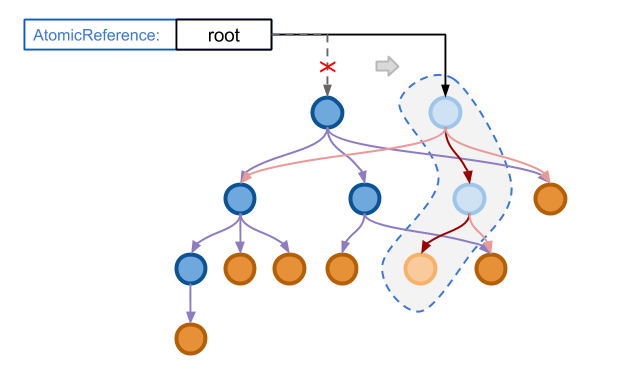
由于对于引用的操作是原子的,因此在原子操作成功之前,任意线程发起的读请求仍然获得的是老的内容, 而一旦这一操作在瞬间完成,所有新的访问都将获得新的内容。不会有任何一个线程会获得中间状态, 这也就保证了多线程环境下的数据安全。
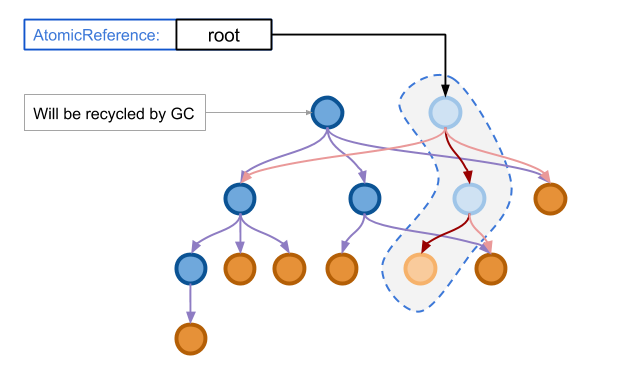
当原子操作执行结束之后,我们可以再清理老的数据结构遗留下来的内存,这一操作也完全可以异步地在后台执行。
由上面几个步骤的示意图我们可以看到,使用原子操作的无锁数据类型的一些基本的思路是:
- 在进行数据修改操作时尽量不改动之前的部分,因此在修改进行的同时对象仍然是可读的, 而一般的加锁数据结构,在修改的同时往往也要阻塞读操作
- 当修改操作完成之后,使用一个单一的原子操作提交修改,从而使修改生效。这样, 即使修改操作十分复杂,最后是否能够成功完成还是取决于一个单一的操作, 这种四两拨千斤的方法消除了因为意外情况导致操作中断而产生的不可知的结果
- 改变引用的原子操作几乎是瞬时的,修改以及修改之后进行清理工作这两部份内容都可以异步地执行, 不影响对数据结构的访问
有的读者可能会想到,如果有两个修改操作同时进行从而导致了结果的相互覆盖该怎么办?
在实践当中,修改的提交操作往往需要通过CompareAndSet这一元语检查对象有没有在自己进行修改的期间被别人修改过。
如果检查失败,修改操作需要被重复地执行。实际上,在写入压力非常大的情况下,有的线程可能一直无法提交自己的修改。
因此,实际上还有一种被称为 Wait-free 的数据结构被研究出来解决这一类问题。
Log-Structured Merge Tree
在本文的最后一个部分要讨论一个比较复杂的数据结构,Log-Structured Merge Tree (简称 LSMT)。 为了更好的介绍它的价值,我们先提出一个非常困难的课题: 如何设计实现一个大数据仓库的储存系统。
设计一个这样的一个储存系统是非常困难的,原因在于要实现以下设计目标:
- 支持对数据字段的增删改查,数据字段的长度可以是变长的
- 支持安全的并发读写,并发的读写操作必须可以高性能地执行
- 超高的稳定性,即使在数据写入的中途因故障中断,也不可以丢失、损坏已有的数据
我们的储存系统在实现的过程当中面临以下挑战:
- 储存空间的组织问题: 由于数据的长度是可变的,如果一个字段的值一开始只有10个字节长,随后要被扩展到数百个字节, 而前后已经没有空闲的空间要怎么办?由于数据支持删除,如果经过一段时间,储存空间当中存在出现了很多空洞该怎么回收?
- 并发实现的问题,因为所有这些增删改查的操作都是并发执行的,怎样才能保证这些并发有序地执行从而不会破坏数据? 结合上一个问题,我们怎么样才能安全的回收空闲空间而不会干扰其他操作的执行?
- 在数据库设计的语境里,即使是单一的一个写硬盘操作也不一定能够被认为是原子的。由于缓冲区的存在和硬件的具体实现不同, 几块数据可能不是以期待的顺序被写入硬盘。此外,即使只有一条记录,也可能在写入一半的时候被断电等因素打断。 我们的数据仓库要具备能在这种情况下也不损坏和丢失已有数据,尽量降低损失的能力
LSMT 就是为了解决这一些问题而被设计出来的。首先,LSMT 基于一个假设: 我们的数据可以在逻辑上以树形组织起来, 就比如在数据库当中,数据可能按照主键以 B+ 树的形式组织起来。其次,LSMT 还吸收了不可变数据结构和无锁数据结构的一些思想,用来保证并发安全性和稳定性。 下图展示了一个 LSMT 数据结构的组织框架:
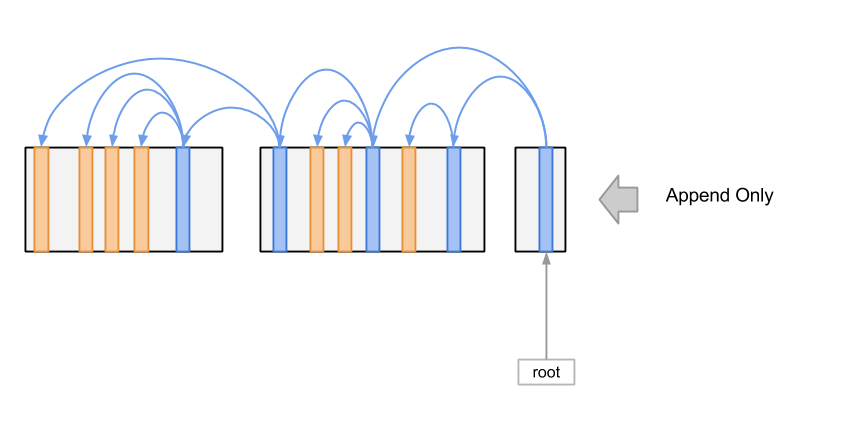
可以看到 LSMT 把所有的数据组织成大小接近的文件块,每个文件块内的记录通过指针引用形成树状的结构, 从而把原始的树形数据结构表示出来。最后 LSMT 还会在外部储存一个指向 Root 节点的指针。 从图中可以看出,LSMT 的写入操作只会有追加一种,对于很多储存介质来说,追加操作要比随机写入快很多, 这也是 LSMT 的优点之一。
接下来我们来看如何把对逻辑树进行的一次修改操作写入到储存中,下图展示了这一操作的基本原理:
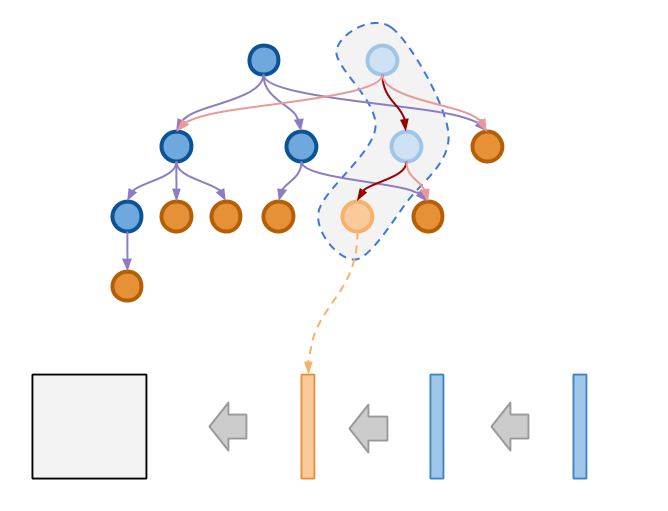
如上图所示,借用 Immutable Tree 的实现思想,当操作执行时,我们会生成一条新的修改路径, 而原来的节点仍然在原来的位置不会被修改。之后我们所做的只是将新产生的节点一个接一个追加到文件的结尾。 追加结束之后的状态如下图所示:
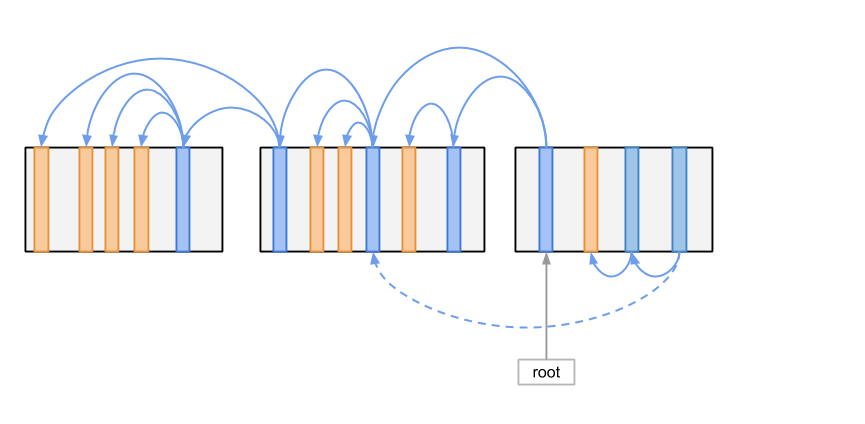
在上图所示的状态时,新的修改其实还没有在储存中生效,新的访问请求到来之后看到的仍然是原来的状态。 这是因为我们的 Root 指针仍然指向原来的根节点。这时就是无锁数据结构实现的思路应用的地方了。 我们可以使用一个接近原子的操作将 Root 指针改向新的根节点。
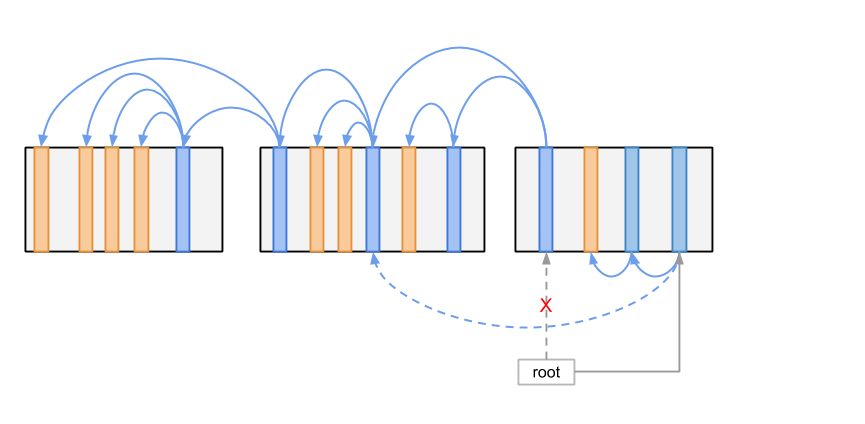
在硬盘等储存介质上进行原子的写入并非十分容易,如果写入 Root 新值的过程被打断怎么办? 其实我们可以把 Root 指针做成类似 Log 的结构,每次只将新值追加到 Log 里,这样之前写成功的值还会得以保留, 如果有一个新值写入中断,我们还可以利用 Log 中之前记录的值恢复到一个有效的状态。 这样移动 Root 指针的操作就可以被认为是原子地执行了。
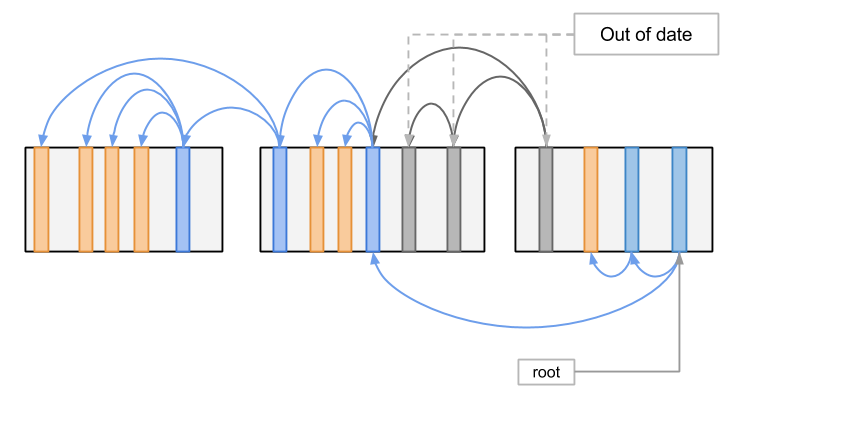
可以看到,新的修改提交成功之后,老的一些记录就变成失效的了,为了清理这些失效的记录, LSMT 还设计在后台执行清理操作,清理的操作逻辑也很简单:
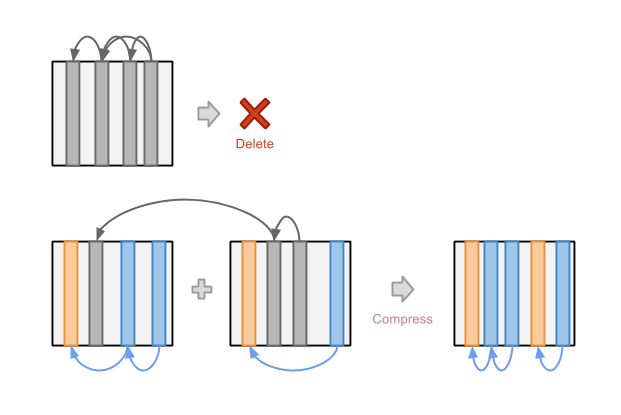
对于一个只包含失效记录的文件,将其直接删除自然是安全的。对于仍然包含有效记录但是已经存在大量失效块的文件, 我们可以采用的策略是将两个这样的文件当中的有效记录取出来合并成一个新的文件。值得注意的是, 在这一步可以重复地利用了 Immutable 和 Lock-free 的实现技巧,在不改变原来文件的情况下先生成新的合并文件, 待合并文件生成完成且生效之后,原来的两个文件就变成了只包含失效记录的文件,可以被安全的删除。
通过执行这样的流程和策略,即使是在高强度的并发条件下,空间的回收操作也可以较为容易地实现。 而且在回收过程当中对数据的读写都不会产生影响。
通过以上的介绍,我们可以看出 LSMT 很好地解决了我们所面临的储存空间组织、并发控制和稳定性等问题, 可以说是实现大数据仓库储存系统的理想数据结构和算法。实际上,包括 BigTable、Apache Cassandra 和 InfluxDB 等产品都利用了 LSMT。
值得注意的是,本文所介绍的只是 LSMT 最简略和基础的一些思想,和真正的 LSMT还有很大的差别。 LSMT 的完整实现还需要解决很多复杂的问题。
总结
本文从对不可变数据结构和无锁数据结构的一些简单思路的介绍开始,最终引入了在数据储存方面非常有价值的一种数据结构 Log-Structured Merge Tree 的介绍。可以看出,即使是一些非常简单的算法技巧,经过巧妙地组合之后也可以发挥非常巨大的作用。
同时,本文也希望通过对这些简单算法的介绍,使得各位读者能够发现和认可算法本身的价值。 算法并不是什么“不会在工作中使用到的东西”。算法是可以为个人和社会都创造巨大收益的重要知识。
