图解图算法 Pregel: 模型简介与实战案例
这篇文章是对之前在 SHLUG 月度分享活动上所作演讲 Pregel in Graphs 的总结。为使分享内容清晰易懂,本人绘制了大量原创示意图,这篇文字版的总结也会尽量以这些图示为主。 除了对 Pregel 算法的简单介绍,本文还附加了一个用户追踪画像的实战案例,用以证明图计算模型的重要意义。
Pregel 简介
Pregel 是 Google 自 2009 年开始对外公开的图计算算法和系统, 主要用于解决无法在单机环境下计算的大规模图论计算问题。与其说 Pregel 是图计算的算法, 不如说它是一系列算法、模型和系统设计组合在一起形成的一套图模型处理方案。
图计算的实际应用非常广泛,因此自 Pregel 公开之后,一些开源的方案也被实现出来, 比如说来自 Spark 的 GraphX 就实现了 PregelAPI。 值得注意的是,Pregel 作为一个近十年前起就为人所知的算法,虽然新近也已经提出了不少增强和改进的技术, 但在现实场景下仍然是很有生命力的。
本文假定读者有基本的图论知识。
模型简介
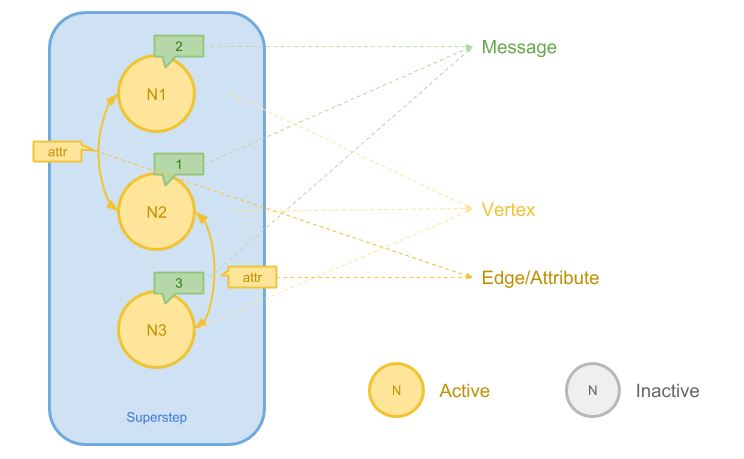
上图展示了 Pregel 计算模型的基本要素,主要包括:
- 节点(Vertex)。在 Pregel 中,每个节点都有全局唯一的 ID
- 边(Edge)。在 Pregel 中,每个边可以被 Assign 一个属性,这个属性可以是边的权值等信息
- 消息(Message)。消息是 Pregel 计算模型的核心。每个 Vertex 在初始状态以及之后的每一个计算步骤当中都被 Attach 一个 Message 值作为 Vertex 当前的状态,算法的迭代通过 Vertex 之间互相发送的消息来完成
- 超迭代(Superstep)。一个 Superstep 是 Pregel 在执行算法过程当中进行的一次迭代。 一次 Pregel 计算过程可能包括多个 Superstep
在 Pregel 当中,Edge 一般是有向的。同时节点 Vertex 还存在 Active 和 Inactive 两种状态。 之后可以看到,节点的状态将会决定一些算法是否结束。
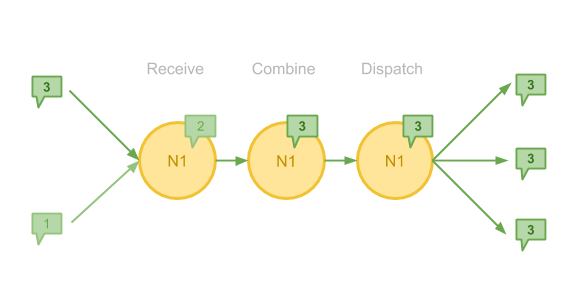
Pregel 的图计算过程与 MapReduce 非常接近:在迭代的每一个步骤当中, 将会以图的节点为中心进行 Map 操作,这意味着在 Map 函数当中我们只有以某一节点为中心的局部信息, 这包括:
- 一个 Vertex 和它当前 Attach 的 Message
- 当前 Vertex 向外指向的 Edge 和 Edge 上的属性
- 当前 Vertex 在上一步计算当中所接收到的全部 Message
对于图中的每一个 Vertex,在 Pregel 当中的一次 Superstep 包括接收消息、合并消息和发送消息三个步骤。 上图当中,节点 N1 接收到了两条 Message ,加上自己原有的 Message,合并出一个最大值, 在最后它会把这个值以消息的形式发送给与之相邻的 Vertex。
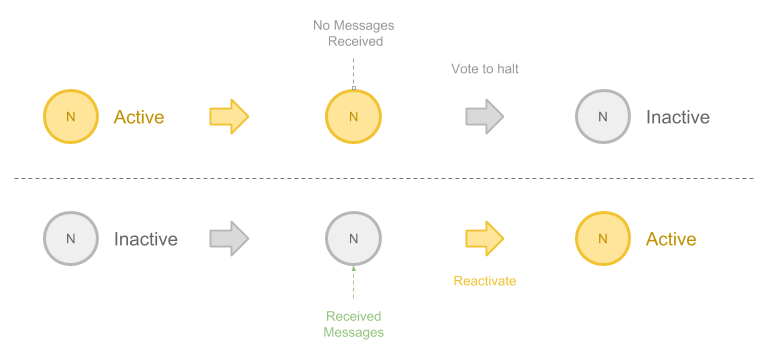
前面提到 Vertex 会有状态变化,这个概念也十分简单:
- 当一个 Vertex 在上一步当中没有接收到消息,或者算法自己决定不再向外发送消息,它可以被转变为 Inactive 的。 在 Pregel 的术语当中,这被称为 Vote to halt
- 当一个在之前已经 Inactive 的 Vertex 又接受到一条新的消息,它会在新的计算中转变为 Active 的状态
在大多数算法当中,所有的 Vertex 都进入 Inactive 状态就意味着算法结束。
下图给出了节点之间传递消息的一个示意,此时 Pregel 还面临一个比较重要的问题: 通过网络发送大量 Message 的成本较高。
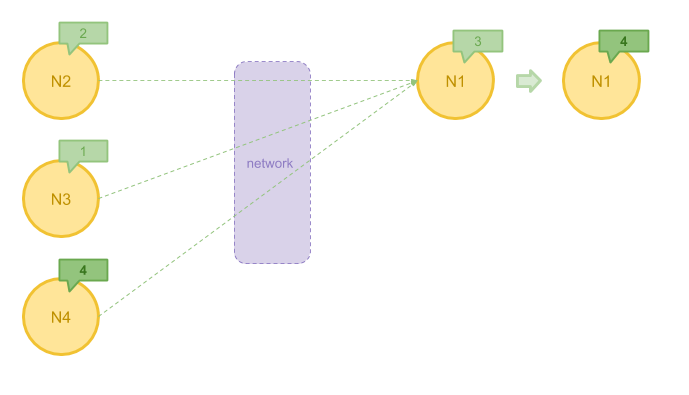
在有些情况下,我们可以在 Message 发送前先对他们进行一步聚合。比方说, 在算法中我们只关心接收到消息的最大值,那么与其把所有消息都发送到目的地再计算, 不如先将最大值求出,这样可以极大地减少需要发送的消息数量。 Pregel 允许用户自定义 Combiner 来实现这一目的。
下图展示了使用 Combiner 聚合左边节点发送的消息的最大值 4 ,之后再发往目标节点的过程。
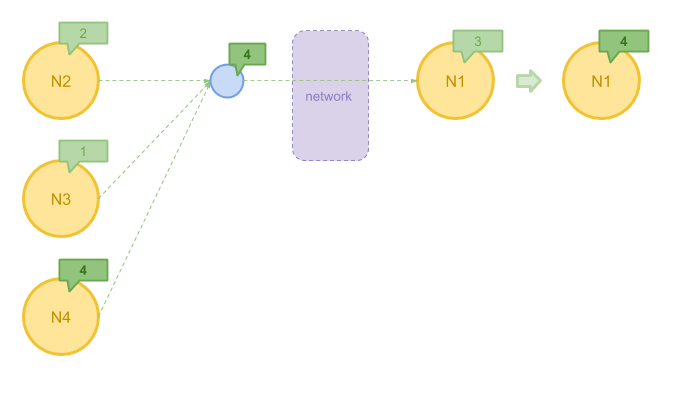
Pregel 需要解决的另一个问题是部分图论算法无法使用上述 Vertex 状态来判断是否结束。 有些时候我们可能需要全图的所有节点共同提供一些信息,统计出一些指标来进行判断。 在另一些情况下,我们也希望对算法的进展进行衡量和追踪。因此,Pregel 还引入了 Aggregator。
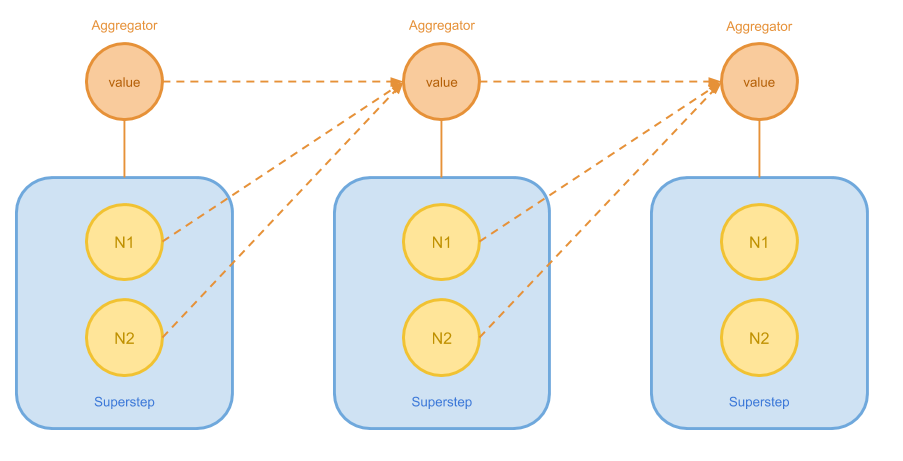
最后一个需要解决的问题是改变拓扑的问题。有些图算法在迭代过程中需要增删节点和边。 Pregel 并没有中心服务掌控整个图的状态,这一需求也被抽象为 Message 发送机制得以解决。
下图中节点 N1 向节点 N2 发送了删除 E1 的指令和向节点 N3 发送了删除节点的指令。 当 N3 被删除之后,其向外的边也都会被一并删除。
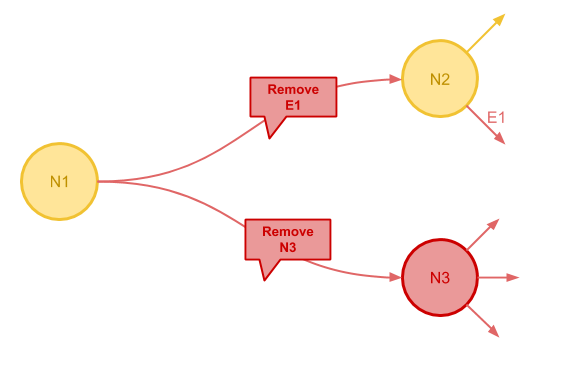
为了防止接收到的拓扑修改的消息相互冲突,这些消息会按照一定的顺序被应用, 用户也可以定义函数用来进行冲突处理。
系统设计
Pregel 的计算模型不单单只有上面介绍的抽象模型而已,为了能在大规模分布式环境下执行这一算法, Pregel 还包含系统设计上的具体考量,比较重要的四条是:
- 将图分区到不同机器进行计算
- 使用主从模型进行任务调度和管理
- 使用 Message 缓冲近一步提高通讯吞吐量
- 使用 Checkpoint 和 Confined Recovery 实现容错性
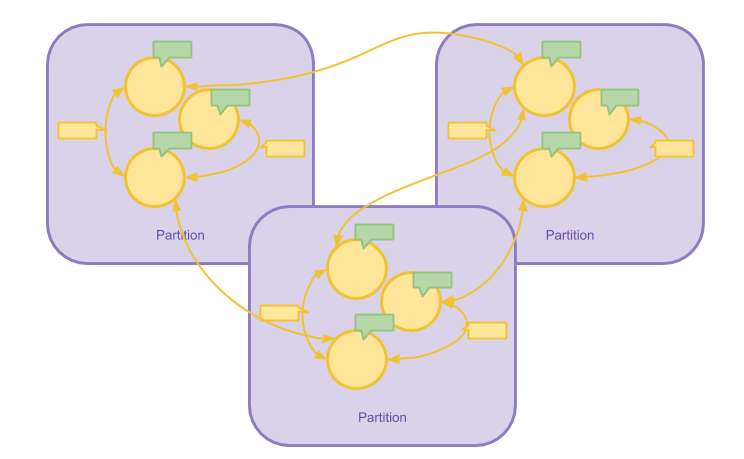
图分区的方法十分容易理解,前文提到 Pregel 是以 Vertex 为中心的计算模型, 因此在分区的时候也是以 Vertex 为中心。 当一个节点被划分到一个区,与之相连的局部信息(边、边属性、消息)也都会被分配到这个区上。 由于对图进行分区的函数是全局一致的,各个计算节点对消息的转发并不需要通过某一中心服务进行协调。
默认的分区方法就是对 VertexId 的 Hash 值进行取模操作。用户也可以自定义分区函数以增强分区的局部性(Locality), 减少计算节点之间的网络流量。
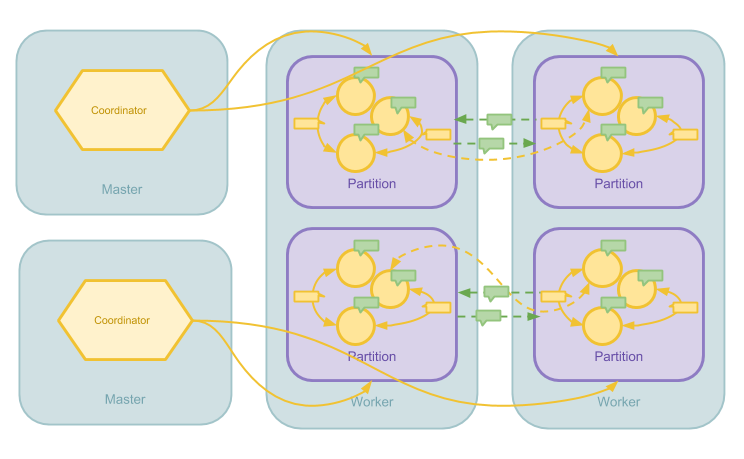
Pregel 在分布式系统当中的任务调度是简单的主从模型。每个计算任务有一个 Master 进程协调所有计算,在每个 Superstep 当中,Master 会决定图分区、发送 RPC 调用到 Worker 节点激发任务以及监控任务完成。所有图分区都在 Worker 上,Master 不管理任何图分区。 不过,Pregel 的 Aggregator 运行在 Master 上。因此 Worker 需要将 Aggregator 所需信息发送到 Master 上进行聚合。
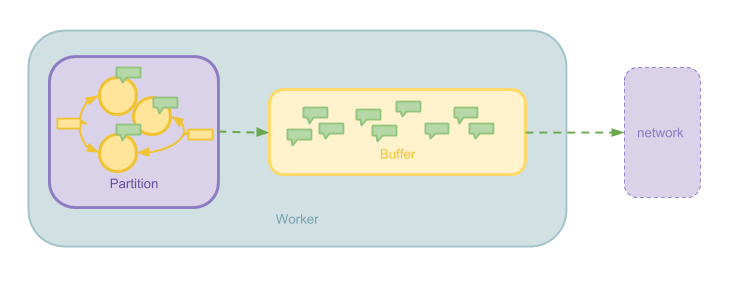
Message 缓冲是在计算节点(Worker)的层面上提高吞吐量的一个优化。 Message 在 Worker 之间传递时并不是来一个发一个,而是通过缓冲积攒一些 Message,之后以 Batch 的形式批量发送。 这一优化可以减少网络请求的 Overhead。
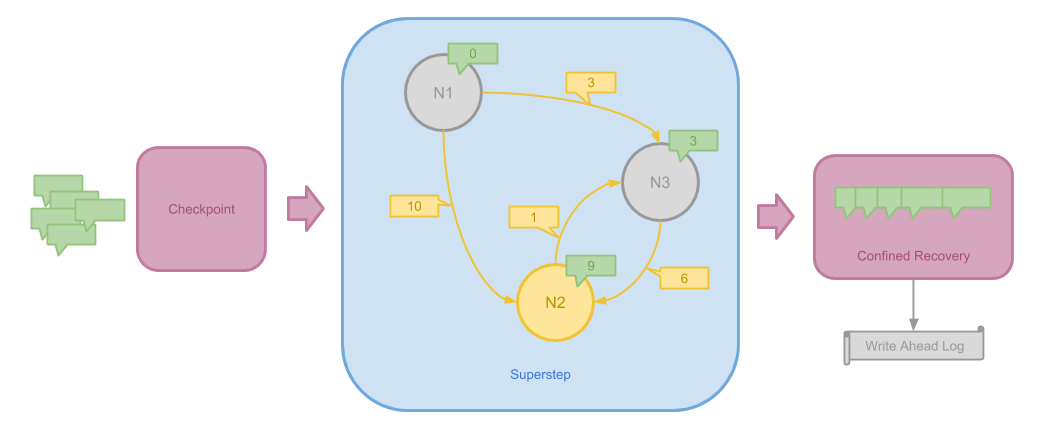
Pregel 使用两种方法来实现容错性:
- Checkpoint 在 Superstep 执行前进行,用来保存当前系统的状态。当某一图分区计算失败但 Worker 仍然可用时, 可以从 Checkpoint 执行快速恢复
- 当某一 Worker 整体失败当机使得它所记录的全部状态丢失时,新启动的 Worker 可能要重新接收上一步发送出来的消息。 为了避免无限制的递归重新计算之前的步骤,Pregel 将 Worker 将要发送的每一条消息写入 Write Ahead Log。 这种方法被称为 Confined Recovery
可以看到,Confined Recovery 的思想和 Spark 等基于 DAG 的计算模型有很多相似的地方。
算法案例
为了使大家对 Pregel 具有更加直观的认识,这一章将介绍一些抽象的算法在 Pregel 之下的运行过程。 对实战案例更感兴趣的朋友可以直接跳到下一章。
计算连通分量
计算连通分量的经典单机算法是并查集, 在 Pregel 中,这一算法通过发送消息的方法实现。
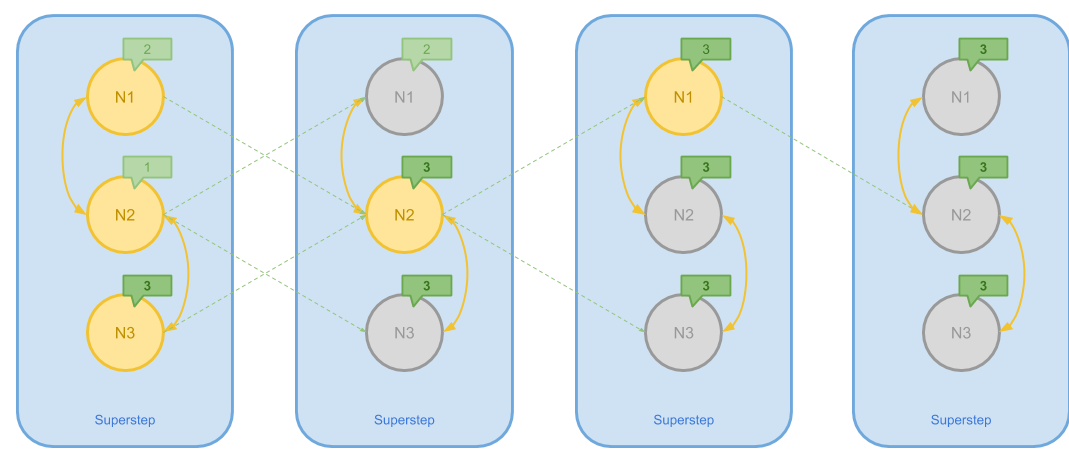
上图提供了 Pregel 计算连通分量的简单过程,其步骤是:
- 为每个节点初始化一个唯一的 Message 值作为初始值
- 在每一个步骤当中,一个 Vertex 将其本身和接收到的 Message 聚合为它们之中的最大值(最小值)
- 如果 Attach 在某一个 Vertex 上的 Message 在上一步当中变大(变小)了, 它就会把新的值发送给所有相邻的节点,否则它会执行 Vote to halt 来 Inactivate 自己
- 算法一直执行直到所有节点都 Inactive 为止
上述连通分量的算法假定边都是双向的(可以通过两条相反的边实现)。可以想像, 由于同一连通分量当中的节点都可以互相传播消息,因此最终在同一个连通分量里的 Vertex, 必定都会拥有这一连通分量内 Message 的最大值(最小值)。这个最后的值就可以作为这一连通分量的 Identifier。
值得注意的是,Pregel 实现的连通分量算法在超大规模的图上仍然有可扩展性的瓶颈, Google 之后发表了论文 Connected Components in MapReduce and Beyond 加以解决。
计算单源最短路
最短路的经典单机算法包括 Dijkstra、 Bellman-Ford 等。 在图规模巨大无法被放入内存的场景下,看到 Pregel 的消息传递模型仍然适用。具体的方法是:
- 初始化 Vertex 的 Message 为 INF (无穷大)
- 将源点的 Message 设为 0
- 每次每个节点将自己目前的 Message 加上边的权值发送到相邻节点,每个节点聚合出自身所有消息的最小值
- 当某一步当中一个节点的 Message 值没有变小,这个节点 Vote to halt
- 当所有节点都 Inactive 时,算法结束
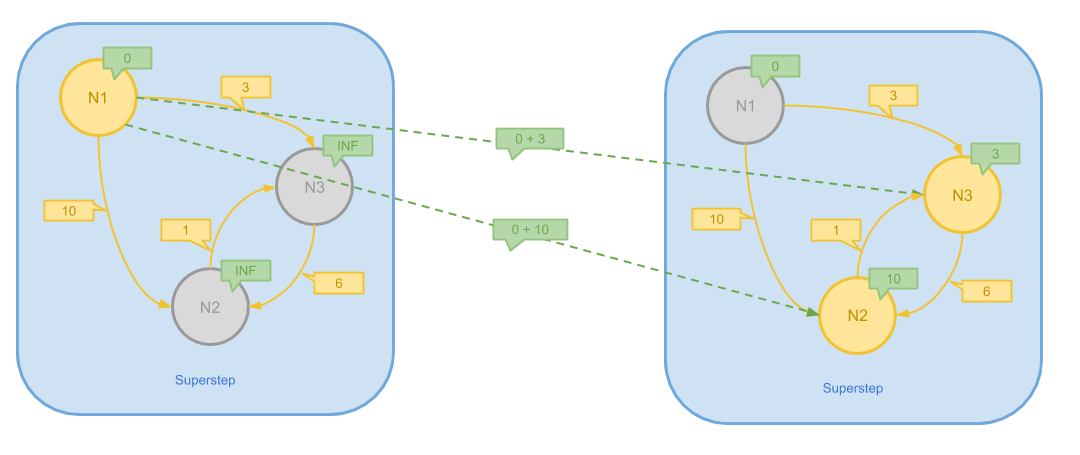
上图展示了一个简单的图最短路的第一步计算步骤,在这一步中,N2、N3 接收到 N1 发送的消息, 从而更新了自己的消息为更小的值。执行结束后,N1 因为没有变化而 Inactive
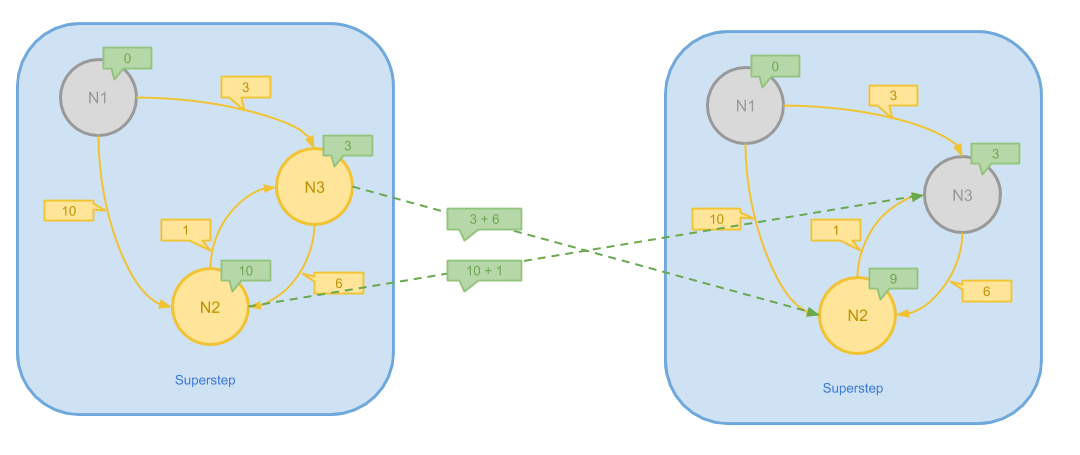
在这一步中,N2 和 N3 户想发送消息,由于 N1 -> N3 -> N2 的路径更短,N3 的 Message 被更新, N2 则变为 Inactive。
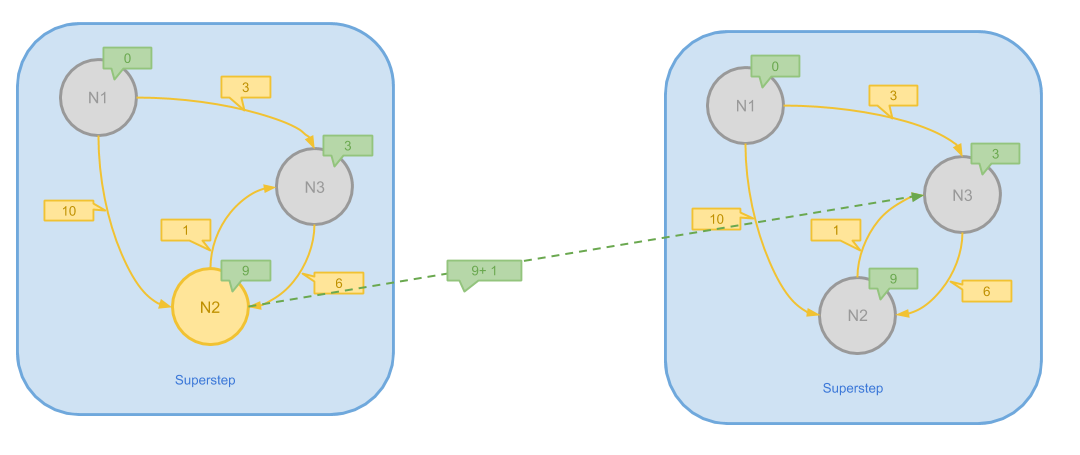
尽管这时所有的最短距离已经求出,由于 N2 在上一步仍然是 Active 的状态,它将会向 N3 发送最后一次消息。 由于 N3 没有更新自己的值,此时图中三个节点都变味 Inactive,算法结束。
PageRank
PageRank 可能是 Pregel 最典型的应用案例。 因为它本身的原理就是通过不断将自身的权值以消息的形式发送出去而完成计算的。
这里拿 PageRank 作为典型案例的原因在于: PageRank 不能简单的以 Vertex 的状态作为算法终止的条件。 除了设定固定的迭代次数之外,另一个方法就是利用 Pregel 的 Aggregator 来跟踪计算过程。
关于 PageRank 的消息传递方法这里不再赘述,下图给出了在一个简单的图上进行计算过程的前半部分:
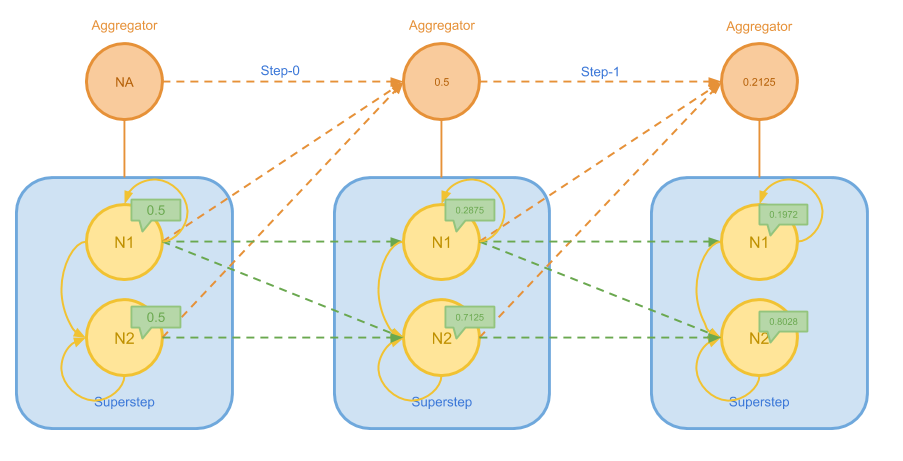
在上图中,N1 不断地将权值发送给自己和 N2,而 N2 则只会发给自己。 随着逐步的迭代,N1 的权值越来越小,N2 的权值越来越大。我们用 Aggregator 跟踪每个节点上权值变化绝对值的最大值 delta,这个最大值会随着迭代的进程而越变越小。
如果我们设定 delta 小于 0.05 时算法结束,则我们将在接下来的步骤中看到如下过程:
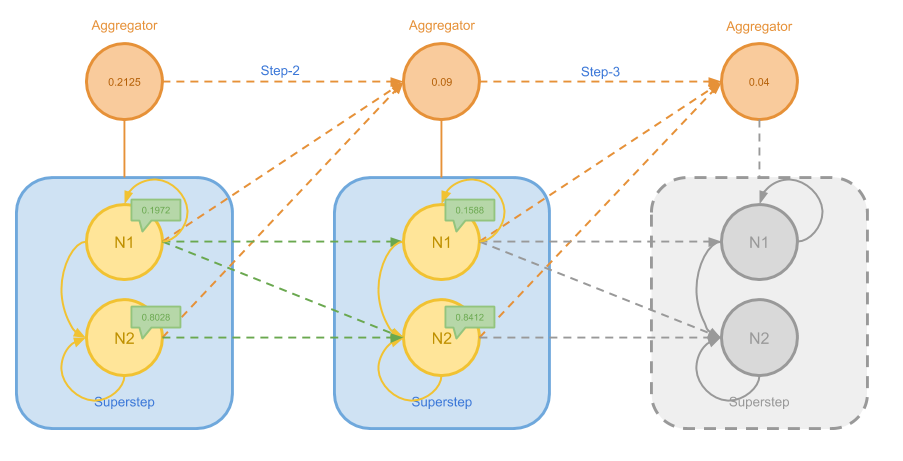
在最后 Aggregator 得到 delta 满足终止条件之后,Master 就可以觉得结束算法了。
实战案例: 用户追踪画像
Pregel 算法的普适性非常强,几乎可以应用各类经典图论算法, 然而我们实际使用它时,主要看中的是它可以解决规模超大的图计算问题。 在这一章我们研究一个实战案例以说明其应用价值。
![]()
上图是我们实战案例的问题描述,具体来说:
- 我们的网站可以收集到各个用户一系列离散的访问请求
- 这些请求可以被以 Session 形式组织起来
- 在一个 Session 的请求当中,我们可能收集到用户各种信息的一个子集
- 我们希望通过一个用户的多个 Session,尽可能聚合到这个用户完整的信息
上面的第三条是我们达成目标的最大阻碍,其原因在于,为了最好的用户体验, 我们不希望在一开始就强迫用户登录或提供定位权限以获得他的全部信息。 设想有一个用户,平时一直匿名访问我们的网站,当有一天他终于认为我们的网站很有价值, 决定注册登陆我们的网站,这时一个典型的需求就是将其之前匿名的访问记录和之后登录的用户联系起来, 从而获得更加有用的信息。
用户追踪画像的基本过程可以分为多个步骤,下图展示了对相互穿插的离散的用户信息的初步处理。
![]()
这一出步处理的主要目的是将离散的请求组织成 Session 的形式并提取出特征。 在这一步之后,我们可以得到很多相互独立的 Session,但是我们仍然不知道哪些 Session 是属于同一个用户的。但是依靠每个 Session 之中提取出来的特征,发现 Session 之间相互的关系是可能的。 如果我们将 Session 作为图的节点,将相互匹配的 Session 用边连接起来, 就可以把用户追踪画像的问题转换为寻找无向图连通分量的问题。
![]()
通过联系和聚合多个 Session 包含的特征,我们得到了比仅着眼单个 Session 更全面的用户信息, 这样用户追踪和画像的问题就解决了。由于网站的用户访问可能是海量的, 这一问题可能必须交由大规模分布式系统进行计算,这即是 Pregel 的用武之处。
在这里有一点扩展优化。设想我们有 $O(N)$ 个 Session,要找出它们两两之间的关系, 需要耗费的是 $O(N^2)$ 的时间,这对于仅有 $10^6$ 个 Session 的规模都是相当不可行的。 我所想到的一种优化是:
- 只选择 $n$ 个重要的特征作为参考
- 定义两个 Session 是匹配的,当有大于等于 $x$ 个特征相匹配
- 对于收集到的一个 Session 的特征,枚举它恰好 $x$ 个特征的子集合
- 匹配这些包含恰好 $x$ 个特征的子集合,而不是 Session 本身
下图展示了这个过程:
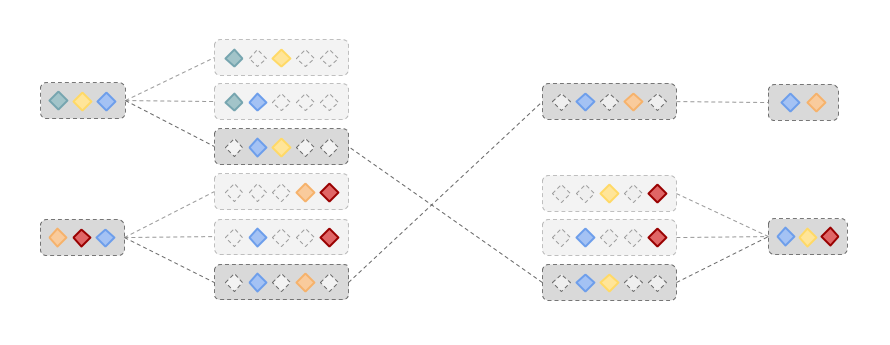
假设 $n=5$ 且 $x=2$,也就是说对于任意两个 Session,我们只考虑它们所拥有的 5 个固定的特征, 当等于或大于 2 个特征匹配,我们就认为两个 Session 匹配。如果我们有 $O(N)$ 个 Session, 因 $\mathtt{C}^2_5=10$ 那么我们将会得到 $O(10\times N)$ 个这样的子集合。
这么做难道不是使得问题的规模上升了么?为什么我们可以算的更快呢? 这是因为这些子集合都恰好包含两个元素,假如我们对这些子集合进行排序, 相同的子集合一定排在一起,这样我们就可以通过在排好序的序列当中, 链接相邻相同子集合所代表的 Session,快速将所有匹配的 Session 连接起来。
对 $O(10\times N)$ 个元素进行排序,将会花费 $O(10\times N\cdot\log (10\times N))$, 最后处理整个序列还需要 $(10\times N)$ 的时间。但是总体的时间复杂度却降低到了 $O(N\log N)$ 的级别,对于 $O(N^2)$ 来说是一个巨大的进步。
换句话说,我们利用类似在终端中使用 sort | uniq 的方式,降低了寻找 Session 匹配的复杂度。
总结
本文简要介绍了 Pregel 的基本模型和系统设计,给出了一些简单算法案例的执行过程。 在最后使用用户追踪画像这样的实战案例,说明了图计算在现实世界当中的具体应用。
着我们需要处理的问题规模越来越大,像 Pregel 这样的分布式计算模型的应用价值也会越来越高,甚至有可能会逐渐超过传统的算法。
然而,在实战案例的扩展优化当中可以看到,那些传统和经典的算法技巧, 在大规模分布式数据处理当中仍然可以发挥启发性的作用。我认为,无论统治未来是 AI 还是区块链, 这些基础的算法技能都是非常重要的。
