Functional Go: Vector Trie 的实现

2016-09-15

上一篇文章介绍了多种实现函数式编程当中持久化数据结构的思路，其中重点对 Vector Trie 这种数据结构的实现原理进行了解释。这一次我们就使用 Golang 来初步地实现这种数据结构。

这篇文章是系列文章的一部分，如果还没有浏览过文章的其它部分请参考：

首先我们来回顾一下 Vector Trie 的设计思路，为了代替 ArrayList 这种数据结构以及兼顾高性能的随机访问和内存使用， Vector Trie 主要采用了以下几种设计：

将 ArrayList 连续的地址空间切分成一段一段定长的数组
使用 Trie 树结构将这些分段组织起来
读取和写入的时候，利用 Trie 树检索的方法查找目标元素所在的位置

值得注意的是，Vector Trie 作为一种高效的 ArrayList 替代，并非一定要用来实现持久化操作，在这篇文章当中，我们将会先完成一个不具备持久化能力的 Vector Trie 实现。将 Vector Trie 转变为不可变数据结构以及 Transient 的实现将会留作下一篇文章的内容。

List 的设计

首先我们定义一些常数：

const (
    SHIFT     = 5
    NODE_SIZE = (1 << SHIFT)
    MASK      = NODE_SIZE - 1
)

其中，NODE_SIZE 是 List 内部节点的宽度，这里我们选用了通用的$2^{5}$，也就是 32 作为 Trie 树节点的宽度。这意味着每个 Trie 树节点将会最多有 32 个子节点。SHIFT 和 MASK 这两个常数将会在我们实现 Trie 树的过程中被用到。

我们将要完成的 List 在 Golang 下接口定义是:

type List interface {
    Get(n int) (interface{}, bool)
    Set(n int, value interface{})
    PushBack(value interface{})
    RemoveBack() interface{}
    Len() int
}

在这一步我们还未考虑持久化的实现，每个操作会直接在原来的基础上进行修改，因此在这里不会返回新的对象。可以看到，目前的 List 定义非常简单，只包含四种基本的操作和获取当前 List 长度的 Len 方法。

由于我们的 List 是以 Trie 树为基础的，先给出 Trie 节点的定义和构造函数：

type trieNode struct {
    children []interface{}
} 

func newTrieNode() *trieNode {
    return &trieNode{
        children: make([]interface{}, NODE_SIZE),
    }
}

可以看到目前为止我们的内部节点非常简单，结构体只包含一个数组用来保存子节点。我们要将 List 的值元素保存在 Trie 树最底层的叶子节点，因此使用了interface{}这种通用类型的数组。这样我们就既可以使用它指向子节点，又可以用来保存值元素。在这里我为trieNode编写了两个方便的工具函数来分别获取子节点和值。

func (node *trieNode) getChildNode(index int) *trieNode {
    if child := node.children[index]; child != nil {
        return child.(*trieNode)
    } else {
        return nil
    }
}

func (node *trieNode) getChildValue(index int) interface{} {
    return node.children[index]
}

由于在 Trie 树的内部节点中，最底层保存的是值，其它节点的children数组则保存指向子节点的引用，维护和记录 Trie 树的高度level是必要的。通过level的值访问 Trie 树的时候我们就可以知道什么时候改获取子节点，什么时候该获得值。这个level在查询 Trie 树的时候也很有用。

作为访问 List 元素的入口，我们数据的 Head 的定义如下:

type listHead struct {
    len    int
    level  int
    root   *trieNode
}

这一结构体保存了 List 的长度、Trie 树的深度以及 Trie 树根节点的引用等信息，我们所有的 List 操作都将会由listHead 来实现，因此它必须服从我们的List接口。

listHead的构造函数就是List的构造函数，在这里我们返回一个空的listHead:

1
2
3

func New() List {
    return &listHead{0, 0, nil}
}

在上述定义下，我们的List实现具有如下图所示的结构:

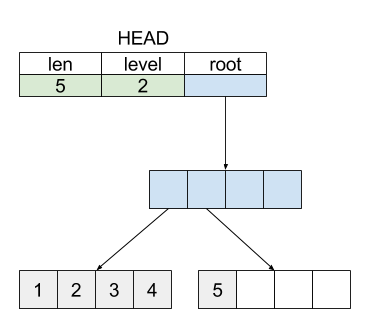
Vector Trie

为了简便起见，图中的 TrieNode 宽度只有 4。在这一结构的基础上，我们就可以实现 List 的一些基本操作了。

`Get` 和 `Set`

我们先来看 Vector Trie 的查询和修改操作。这两个操作非常相似，都需要根据给定的 Index 在 Trie 树中找到对应的位置，区别在于Get操作将会返回目标位置储存的元素而Set操作将会修改它。

Trie 树的中文名称是前缀树，从这个名字当中就可以一窥这类数据结构的查询方法。简单来说，对于由 $n$ 个 Symbol $s_i$ 组成的关键字 $\mathcal{K}={s_0, s_1, \cdots, s_n}$，我们先使根节点为当前节点，之后使用 $s_0$ 查询得到的子节点作为当前节点，然后再依次使用 $s_1, s_2, \cdots$ 在当前节点上查询得到的子节点作为当前节点，得到一个最终节点作为结果。

具体来说，在这里用户用来查询的关键字 $\mathcal{K}$ 是一个32位类型的整型数。我们要将这个整形数看作一连串符号的连接，最简单的做法当然是把这个整型树看作其二进制表示，每隔 $m$ 位看作一个独立的符号，这样从这个整型数的二进制表示的高位开始往下，就依次可以被划分成$s_0, s_1, \cdots, s_n$。由此我们也就可以将其用于 Trie 的查询。这也是为什么我们选择 $2^{m}$ 作为 TrieNode 的宽度的原因了，通过使用二进制位运算，我们可以非常快速的从整数当中获得 $s_i$ 的值。在程序中 $m$ 的值由 SHIFT 定义，我们使用 5 作为 $m$，则每个 Symbol 的取值范围则是 $[0, 31]$，恰好是长度 32 的数组当中元素 Index 的范围，得到 Symbol 的值之后，我们可以直接从数组当中取得目标元素。

下图展示了 $m = 2$ 时的这一过程:

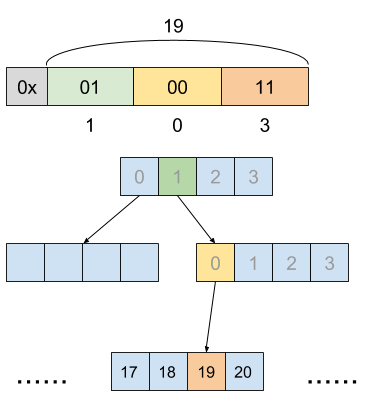
Trie Traverse

另外需要注意的一点是，我们显然不会直接从 32 位的整数的最高位开始编码 $s_i$。原因在于，当数组元素较少时，列表里每个元素的 Index 数值都比较小，因此二进制位表示当中高位基本上都是 0，因此创建这样一连串的只有 0 位置不为空的树是非常不划算的行为，这也是为什么我们要记录和维护当前 Trie 树的高度。

下面给出了 Get 方法的实现。由于 Get 方法是不会修改列表中的元素的，直接使用循环获取到目标元素即可。

func (head *listHead) Get(n int) (interface{}, bool) {
    if n < 0 || n >= head.len {
        return nil, false
    }

    root := head.root
    for lv := head.level - 1; ; lv-- {
    index := (n >> uint(lv*SHIFT)) & MASK
    if lv <= 0 {
        // Arrived at leaves node, return value
        return root.getChildValue(index), true
    } else {
        // Update root node
        root = root.getChildNode(index)
    }
  }
}

Set 操作与之类似，但是我们这里使用递归的方法进行，这样做的目的是为了让 Set 函数在递归调用的每次返回时可以复写当前节点，直至最后复写 root 节点。但是在未来实现持久化的时候，可以通过返回新的节点的方式获得从根节点到叶子节点这条路径的一个副本。

func (head *listHead) Set(n int, value interface{}) {
    if n < 0 || n >= head.len {
        panic("Index out of bound")
    }

    head.root = setInNode(head.root, n, head.level, value)
}

func setInNode(root *trieNode, n int, level int, value interface{}) *trieNode {
    index := (n >> uint((level-1)*SHIFT)) & MASK

    if level == 1 {
        root.children[index] = value
    } else {
        child := root.getChildNode(index)
        root.children[index] = setInNode(child, n, level-1, value)
    }

    return root
}

特别值得注意的是 index = (n >> uint((level - 1)*SHIFT)) & MASK 这一语句了，它根据level的值计算当前应该用来查询子元素的$s_i$，也就是目标子元素在数组中的位置。其中 SHIFT = 5，MASK = (1 << SHIFT) - 1 = 31，MASK的二进制表示从最低位开始向上恰好是 5 个 1，这样我们就把 n 每 5 位一组分为一个 Symbol 进行查询了。

`tail` 优化

可以在 List 当中查询和修改元素之后，我们还需要允许在 List 当中添加和删除元素，不过在此之前，我们要先介绍我们将要采用的一种针对 Vector Trie 的优化手段：tail 优化。

在 Vector Trie 所支持的 4 种基础操作 Get、Set、PushBack和RemoveBack中，只有后两种会修改列表中所储存的元素长度。同时也只有 PushBack 操作可能会分配新的内存空间。由于 PushBack 和 RemoveBack 是 List 所应该支持的高频操作，针对这两个操作进行性能优化是一件很有必要的事情。这两种操作都是直接作用于 List 尾部，参考链表的尾指针的思想，我们容易想到可以直接保留一个指向 Trie 树最末尾元素节点的引用，这样每次对尾部进行操作就不需要进行耗时的 Trie 树查询操作了。

Tail 优化技巧的应用思路如下：

PushBack 和 RemoveBack 操作直接作用于tail指针所指向的 trieNode
PushBack 之前如果当前的 tail 已满，则将tail放回到 Trie 树上再创建一个新的
RemoveBack 之后，如果当前 tail 已空，则释放当前 tail，并将 Trie 树的最后一个 trieNode 取出作为新的 tail

我们总是保持 tail 段非空，也就是说 tail 要么是 nil，代表整个 List 当中没有储存任何元素，要么至少包含一个元素。这样的设计可以简化 RemoveBack 的实现，也可以提高未来可能会提供的 GetLast 等方法的操作性能。

为了实现上述的操作，我们需要维护一个offset值，它代表的是列表中在 tail 节点之前的节点当中储存的元素的数量，同时也是 tail 节点中下标0的元素在整个 List 当中的 Index。在Get、Set操作之时，我们先检查目标 Index 是否大于等于offset，如果为真，我们就直接在 tail 节点上进行操作。否则说明目标元素在 Trie 树当中，我们仍然使用之前的 Trie 树操作。下图展示添加 tail 之后的数据结构：

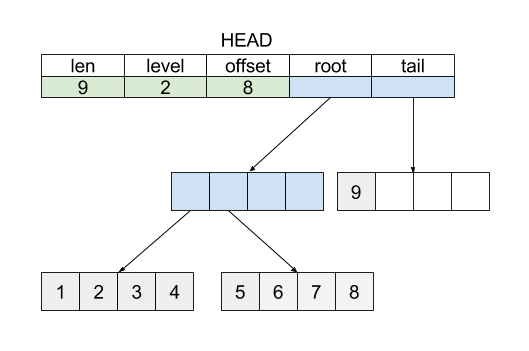
Vector Trie with Tail

修改之后的Get和Set方法如下：

func (head *listHead) Get(n int) (interface{}, bool) {
    if n < 0 || n >= head.len {
        return nil, false
    }

    if n >= head.offset {
        return head.tail.getChildValue(n - head.offset), true
    }

    // Get elements in the trie
    // ...
}

func (head *listHead) Set(n int, value interface{}) {
    if n < 0 || n >= head.len {
        panic("Index out of bound")
    }

    if n >= head.offset {
        head.tail = setTail(head.tail, n-head.offset, value)
    } else {
        head.root = setInNode(head.root, n, head.level, value)
    }
}

func setTail(tail *trieNode, n int, value interface{}) *trieNode {
    if tail == nil {
        tail = newTrieNode()
    }
    tail.children[n] = value
    return tail
}

`PushBack` 和 `RemoveBack`

在加入 tail 之后，我们终于可以开始实现把元素插入和删除的操作了，目前我们只支持从数组尾部添加和删除元素。由于使用了 tail 优化，两个操作的主要实质内容其实都发生在 tail 节点上，但是在这一过程中需要考虑维护tail节点的问题。

如前文所述，我们如果我们在试图进行PushBack的时候tail中的元素已满，那么我们需要将当前的tail节点放入 Trie 中，维护和更新offset的值，然后新建一个tail出来并把元素插入到新的tail上。由于offset是tail当中第一个元素在 List 中的位置，利用这一特点，我们可以在 Trie 树中找出offset位置的元素应该存在的位置，那里自然也就是tail应该被放置的地方。参考setInNode的递归实现，我们容易得到如下代码:

func putTail(root *trieNode, tail *trieNode, n int, level int) *trieNode {
    index := (n >> uint((level-1)*SHIFT)) & MASK

    if root == nil {
        root = newTrieNode()
    }

    if level == 1 {
        return tail
    } else {
        root.children[index] = putTail(root.getChildNode(index), tail, n, level-1)
    }

    return root
}

但是这一步过程当中存在一个问题，那就是如果当前的 Trie 树也是满的，在放入 tail 之时，必须先提高 Trie 树的深度，也就是使 level 增加 $1$。Trie 树等层数增长很容易实现，我们只需要新建一个root节点，然后将原来的root节点设置为新节点的第一个子节点。

那我们该如何判断是否需要进行层增长的操作呢？在这里我们依然要利用offset的特点，由于在增加后的 Trie 树中offset所代表的 Index 将会可以在 Trie 树中查询到，因此对于 Trie 树的高度level，必须满足(offset >> (level * SHIFT)) == 0。通过这个表达式，我们就可以保证在putTail时 Trie 树的层数是足够高的了。

下面的是PushBack的实现代码：

func (head *listHead) PushBack(value interface{}) {
    // Increase the depth of tree while the capacity is not enough
    if head.len-head.offset < NODE_SIZE {
        // Tail node has free space
        head.tail = setTail(head.tail, head.len-head.offset, value)
    } else {
        // Tail node is full
        n := head.offset
        lv := head.level
        root := head.root

        for lv == 0 || (n>>uint(lv*SHIFT)) > 0 {
            parent := newTrieNode()
            parent.children[0] = root
            root = parent
            lv++
        }

        head.root = putTail(root, head.tail, n, lv)
        head.tail = nil
        head.tail = setTail(head.tail, 0, value)

        head.level = lv
        head.offset += NODE_SIZE
    }
    head.len++
}

因为我们会保证tail节点非空，所以RemoveBack也总是作用在tail上。它的实现很容易，需要注意的主要有以下3点:

如果执行RemoveBack之后tail变成空的，则需要从 Trie 树里取出最后一个trieNode作为新的tail
如果执行RemoveBack之后 List 长度变为 0，则直接重置列表到空的状态
如果从 Trie 树中取出节点之后root节点只有一个孩子，那么我们把root节点替换成它的孩子，由此 Trie 的高度减小 $1$

下面是从 Trie 当中获得一个节点的代码:

func getTail(root *trieNode, n int, level int) (*trieNode, *trieNode) {
    index := (n >> uint((level-1)*SHIFT)) & MASK

    if level == 1 {
        return nil, root
    } else {
        child, tail := getTail(root.getChildNode(index), n, level-1)

        if index == 0 && child == nil {
            // The first element has been removed, which means current node
            // becomes empty, remove current node by returning nil
            return nil, tail
        } else {
            // Current node is not empty
            return root, tail
        }
    }
}

为了能使用上述函数获得最后一个trieNode，我们使n = len - 1，也就是最后一个元素 Index。在取出tail之后，我们需要检查 Trie 是否需要降低层数。由于我们总是保证 Trie 树中的元素编号是从 0 开始连续到达offset - 1的，因此如果root只剩下一个孩子，那么它一定是第0号孩子。设 Trie 的高度是level，n = offset - 1，那么也就有 (n>>uint((lv-1)*SHIFT)) == 0为真。通过这个判断我们就可以决定是否降低 Trie 树的层数了。

完整的 RemoveBack 实现如下:

func (head *listHead) RemoveBack() interface{} {
    if head.len == 0 {
        panic("Remove from empty list")
    }

    value := head.tail.getChildValue(head.len - head.offset - 1)
    head.tail = setTail(head.tail, head.len-head.offset-1, nil) // clear reference to release memory

    head.len--

    if head.len == 0 {
        head.level = 0
        head.offset = 0
        head.root = nil
        head.tail = nil
    } else {
        if head.len <= head.offset {
            // tail is empty, retrieve new tail from root
            head.root, head.tail = getTail(head.root, head.len-1, head.level)
            head.offset -= NODE_SIZE
        }

        // Reduce the depth of tree if root only have one child
        n := head.offset - 1
        lv := head.level
        root := head.root

        for lv > 1 && (n>>uint((lv-1)*SHIFT)) == 0 {
            root = root.getChildNode(0)
            lv--
        }

        head.root = root
        head.level = lv
    }

    return value
}

性能测试

至此我们的 Vector Trie 就实现了，虽然持久化的功能尚未完成，但是我们已经拥有了一个可用的 List 容器类。接下来让我们测试一下这一容器的性能。我编写了如下的 Benchmark 代码:

func BenchmarkPushBack(b *testing.B) {
    list := New()
    var v interface{}
    for i := 0; i < b.N; i++ {
        list.PushBack(v)
    }
}

func BenchmarkGet(b *testing.B) {
    mask := (1 << 10) - 1
    list := generateList(0, mask+1, 1)

    for i := 0; i < b.N; i++ {
        list.Get(i & mask)
    }
}

func BenchmarkSet(b *testing.B) {
    mask := (1 << 10) - 1
    list := generateList(0, mask+1, 1)

    var v interface{} = 0

    for i := 0; i < b.N; i++ {
        list.Set(i&mask, v)
    }
}

func BenchmarkRemoveBack(b *testing.B) {
    mask := (1 << 20) - 1
    list := generateList(0, mask+1, 1)

    for i := 0; i < b.N; i++ {
        if list.Len() > 0 {
            list.RemoveBack()
        } else {
            b.StopTimer()
            list = generateList(0, mask+1, 1)
            b.StartTimer()
        }
    }
}

值得注意得是，在 Golang 中将原始数据类型如int等转换为interface{}其实会产生内存分配操作，因此会拖慢程序的运行，为了了解原始的操作性能，Set和PushBack操作使用的都是固定的value。 Get操作则是在一个长度为 $1024$ 的 List 上进行循环的读操作。下面是 Benchmark 的结果:

BenchmarkPushBack-2     20000000           67.8 ns/op       34 B/op     0 allocs/op
BenchmarkGet-2          100000000          11.4 ns/op        0 B/op     0 allocs/op
BenchmarkSet-2          50000000           20.6 ns/op        0 B/op     0 allocs/op
BenchmarkRemoveBack-2   50000000           25.3 ns/op        0 B/op     0 allocs/op

由此可见，我们实现的 Vector trie 在 Get、Set和RemoveBack上的性能比较让人满意，基本控制在30ns以下， PushBack操作的时间略高于预期，经过进一步的分析发现时间主要花费在runtime.scanobject方法上，也就是说 Golang 自己的 GC 性能影响了我们的实现性能。在未来也许可以对我们PushBack时所进行的内存操作进行进一步的优化，从另一个角度来说，Golang 自己的 GC 性能也还有进一步提升的空间。

总结

在这篇文章中，我们初步实现了不带持久化功能的 Vector Trie 并对其进行了简单的性能分析。

从当前的实现中已经可以看到将其转变为不可变数据结构的曙光。在下一篇文章中我们将会继续讨论 Vector Trie，给出将其变化为不可变数据结构的最终实现方法和使其具备高性能读写的 Transient 数据结构的实现。

Programic Creativity

IO METER

Article

Functional Go: Vector Trie 的实现

List 的设计

`Get` 和 `Set`

`tail` 优化

`PushBack` 和 `RemoveBack`

性能测试

总结

Comments

Article

List 的设计

Get 和 Set

tail 优化

PushBack 和 RemoveBack

性能测试

总结

Comments

`Get` 和 `Set`

`tail` 优化

`PushBack` 和 `RemoveBack`